Base Functions¶
EcoPy contains several basic functions:
-
wt_mean(x, wt=None)¶ Calculates as weighted mean. Returns a float.
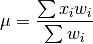
Parameters
- x: numpy.ndarray or list
- A vector of input observations
- wt: numpy.ndarray or list
- A vector of weights. If this vector does not sum to 1, this will be transformed internally by dividing each weight by the sum of weights
Example
Weighted mean:
import ecopy as ep print(ep.wt_mean([1,3,5], [1,2,1]))
-
wt_var(x, wt=None, bias=0)¶ Calculates as weighted variance. Returns a float.
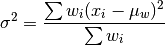
where
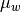 is the weighted mean.
is the weighted mean.Parameters
- x: numpy.ndarray or list
- A vector of input observations
- wt: numpy.ndarray or list
- A vector of weights. If this vector does not sum to 1, this will be transformed internally by dividing each weight by the sum of weights
- bias: [0 | 1]
- Whether or not to calculate unbiased (0) or biased (1) variance. Biased variance is given by the equation above. Unbiased variance is the biased variance multiplied by
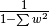 .
.
Example
Weighted variance:
import ecopy as ep print(ep.wt_var([1,3,5], [1,2,1]))
-
wt_scale(x, wt=None, bias=0)¶ Returns a vector of scaled, weighted observations.
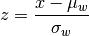
where
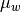 is the weighted mean and
is the weighted mean and 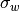 is weighted standard deviation (the square root of weighted variance).
is weighted standard deviation (the square root of weighted variance).Parameters
- x: numpy.ndarray or list
- A vector of input observations
- wt: numpy.ndarray or list
- A vector of weights. If this vector does not sum to 1, this will be transformed internally by dividing each weight by the sum of weights
- bias: [0 | 1]
- Whether or not the weighted standard deviation
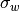 should be calculated from the biased or unbiased variance, as above
should be calculated from the biased or unbiased variance, as above
Example
Weighted variance:
import ecopy as ep print(ep.wt_scale([1,3,5], [1,2,1]))
-
impute(Y, method='mice', m=5, delta=0.0001, niter=100)¶ Performs univariate missing data imputation using one of several methods described below. NOTE: This method will not work with categorical or binary data (see TO-DO list). See van Buuren et al. (2006) and/or van Buuren (2012) for descriptions of univariate, monotone, and MICE algorithms.
Parameters
- Y: numpy.ndarray or pandas.DataFrame
- Data matrix containing missing values. Missing values need not be only in one column and can be in all columns
- method: [‘mean’ | ‘median’ | ‘multi_norm’ | ‘univariate’ | ‘monotone’ | ‘mice’]
Imputation method to be used. One of the following:
mean: Replaces missing values with the mean of their respective columns. Returns a single numpy.ndarray.
median: Replaces missing values with the median of their respective columns. Returns a single numpy.ndarray.
multi_norm: Approximates the multivariate normal distribution using the fully observed data. Replaces missing values with random draws from this distribution. Returns m numpy.ndarrays.
univariate: Conducts univariate imputation based on posterior draws of Bayesian regression parameters.
monotone: Monotone imputation for longitudinally structured data.
mice: Implements the MICE algorithm for data imputation. Assumes the univariate model is the correct model for all columns.
- m: integer
- Number of imputed matrices to return
- delta: float [0.0001 - 0.1]
- Ridge regression parameter to prevent non-invertible matrices.
- niter: integer
- Number of iterations implemented in the MICE algorithm
Example
First, load in the urchin data:
import ecopy as ep import numpy as np import pandas as pd data = ep.load_data('urchins')
Randomly replace mass and respiration values with NAs:
massNA = np.random.randint(0, 24, 5) respNA = np.random.randint(0, 24, 7) data.loc[massNA, 'UrchinMass'] = np.nan data.loc[respNA, 'Respiration'] = np.nan
Impute using the MICE algorithm, then convert the returned arrays to dataframes:
imputedData = ep.impute(data, 'mice') imputedFrame = [pd.DataFrame(x, columns=data.columns) for x in imputedData]
Alternatively, replace the missing values with the column means:
meanImpute = ep.impute(data, 'mean')
-
spatial_median(X)¶ Calculates the spatial median of a multivariate dataset. The spatial median is defined as the multivariate point
 that minimizes:
that minimizes: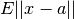
where
 is the euclidean distance between the vector
is the euclidean distance between the vector  and
and  . Minimization is achieved by minimization optimization using scipy.optimize.minimize and the ‘BFGS’ algorithm.
. Minimization is achieved by minimization optimization using scipy.optimize.minimize and the ‘BFGS’ algorithm.Parameters
- X: numpy.ndarray or pandas.DataFrame
- A matrix of input observations
Example
Calculate the spatial median for a random matrix:
import ecopy as ep from scipy.stats import multivariate_normal np.random.seed(654321) cov = np.diag([3.,5.,2.]) data = multivariate_normal.rvs([0,0,0], cov, (100,)) spatialMed = ep.spatial_median(data)