Ordination¶
Ecopy contains numerous methods for ordination, that is, plotting points in reduced space. Techniques include, but are not limited to, principle components analysis (PCA), correspondence analysis (CA), principle coordinates analysis (PCoA), and multidimensional scaling (nMDS).
-
class
pca(x, scale=True, varNames=None)¶ Takes an input matrix and performs principle components analysis. It will accept either pandas.DataFrames or numpy.ndarrays. It returns on object of class :py:class: pca, with several methods and attributes. This function uses SVD and can operate when rows < columns. NOTE: PCA will NOT work with missing observations, as it is up to the user to decide how best to deal with those. Returns object of class
pca.Parameters
- x: a numpy.ndarray or pandas.DataFrame
- A matrix for ordination, where objects are rows and descriptors/variables as columns. Can be either a pandas.DataFrame or numpy. ndarray.
- scale: [True | False]
- Whether or not the columns should be standardized prior to PCA. If ‘True’, the PCA then operates on a correlation matrix, which is appropriate if variables are on different measurement scales. If variables are on the same scale, use ‘False’ to have PCA operate on the covariance matrix.
- varNames: list
- If using a numpy.ndarray, pass a list of column names for to help make PCA output easier to interpret. Column names should be in order of the columns in the matrix. Otherwise, column names are represented as integers during summary.
Attributes
-
evals¶ Eigenvalues in order of largest to smallest.
-
evecs¶ Normalized eigenvectors corresponding to each eigenvalue (i.e. the principle axes).
-
scores¶ Principle component scores of each object (row) on each principle axis. This returns the raw scores
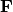 calculated as
calculated as 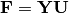 where
where 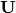 is the matrix of eigenvectors and
is the matrix of eigenvectors and 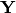 are the original observations.
are the original observations.
Methods
-
classmethod
summary_imp()¶ Returns a data frame containing information about the principle axes.
-
classmethod
summary_rot()¶ Returns a data frame containing information on axes rotations (i.e. the eigenvectors).
-
classmethod
summary_desc()¶ Returns a data frame containing the cumulative variance explained for each predictor along each principle axis.
-
classmethod
biplot(xax=1, yax=2, type='distance', obsNames=False)¶ Create a biplot using a specified transformation.
- xax: integer
- Specifies which PC axis to plot on the x-axis
- yax: integer
- Specifies which PC axis to plot on the y-axis
- type: [‘distance’ | ‘correlation’]
Type ‘distance’ plots the raw scores
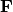 and the raw vectors
and the raw vectors 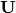 of the first two principle axes.
of the first two principle axes.Type ‘correlation’ plots scores and vectors scaled by the eigenvalues corresponding to each axis:
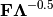 and
and 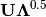 , where
, where 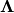 is a diagonal matrix containing the eigenvalues.
is a diagonal matrix containing the eigenvalues.- obsNames: [True | False]
- Denotes whether to plot a scatterplot of points (False) or to actually show the names of the observations, as taken from the DataFrame index (True).
Examples
Principle components analysis of the USArrests data. First, load the data:
import ecopy as ep USArrests = ep.load_data('USArrests') USArrests.set_index('State', inplace=True)
Next, run the PCA:
arrests_PCA = ep.pca(USArrests, scale=True)
Check the importance of the different axes by examining the standard deviations, which are the square root of the eigenvalues, and the proportions of variance explained by each axis:
impPC = arrests_PCA.summary_imp() print(impPC) PC1 PC2 PC3 PC4 Std Dev 1.574878 0.994869 0.597129 0.416449 Proportion 0.620060 0.247441 0.089141 0.043358 Cum Prop 0.620060 0.867502 0.956642 1.000000
Next, examine the eigenvectors and loadings to determine which variables contribute to which axes:
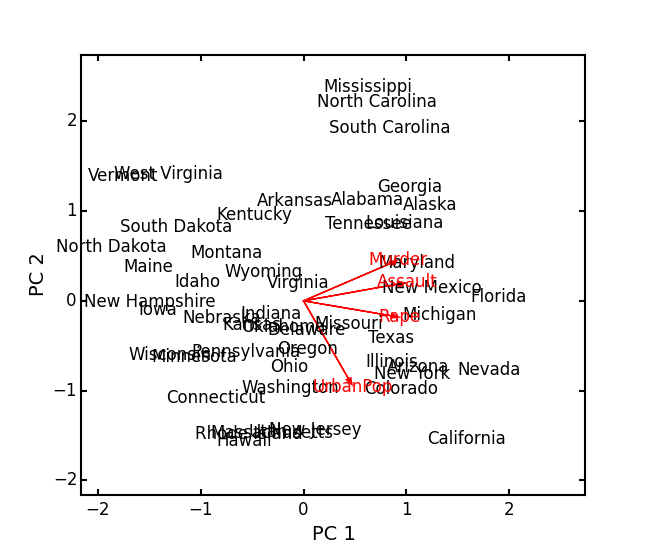
rotPC = arrests_PCA.summary_rot() print(rotPC) PC1 PC2 PC3 PC4 Murder 0.535899 0.418181 -0.341233 0.649228 Assault 0.583184 0.187986 -0.268148 -0.743407 UrbanPop 0.278191 -0.872806 -0.378016 0.133878 Rape 0.543432 -0.167319 0.817778 0.089024
Then, look to see how much of the variance among predictors is explained by the first two axes:
print(arrests_PCA.summary_desc()) PC1 PC2 PC3 PC4 Murder 0.712296 0.885382 0.926900 1 Assault 0.843538 0.878515 0.904153 1 Urban Pop 0.191946 0.945940 0.996892 1 Rape 0.732461 0.760170 0.998626 1
Show the biplot using the ‘correlation’ scaling. Instead of just a scatterplot, use obsNames=True to show the actual names of observations:
arrests_PCA.biplot(type='correlation', obsNames=True)
-
class
ca(x, siteNames=None, spNames=None, scaling=1)¶ Takes an input matrix and performs principle simple correspondence analysis. It will accept either pandas.DataFrames or numpy.ndarrays. Data MUST be 0’s or positive numbers. NOTE: Will NOT work with missing observations, as it is up to the user to decide how best to deal with those. Returns on object of class
ca.Parameters
- x: a numpy.ndarray or pandas.DataFrame
A matrix for ordination, where objects are rows and descriptors/variables as columns. Can be either a pandas.DataFrame or numpy.ndarray. NOTE: If the matrix has more variables (columns) than objects (rows), the matrix will be transposed prior to analysis, which reverses the meanings of the matrices as noted.
The matrix is first scaled to proportions by dividing each element by the matrix sum,
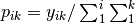 . Row (site) weights
. Row (site) weights 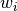 are calculated as the sums of row probabilities and column (species) weights
are calculated as the sums of row probabilities and column (species) weights 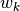 are the sum of column probabilities. NOTE: If
are the sum of column probabilities. NOTE: If 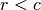 in the original matrix, then row weights give species weights and column weights give site weights due to transposition.
in the original matrix, then row weights give species weights and column weights give site weights due to transposition.A matrix of chi-squared deviations is then calculated as:
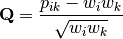
This is then converted into a sum-of-squared deviations as
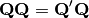
Eigen-decomposition of
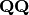 yields a diagonal matrix of eigenvalues
yields a diagonal matrix of eigenvalues 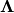 and a matrix of eigenvectors
and a matrix of eigenvectors 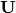 . Left-hand eigenvectors
. Left-hand eigenvectors 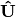 (as determined by SVD) are calculated as
(as determined by SVD) are calculated as 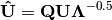 .
. 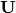 gives the column (species) loadings and
gives the column (species) loadings and 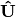 gives the row (site) loadings. NOTE: If
gives the row (site) loadings. NOTE: If 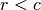 in the original matrix, the roles of these matrices are reversed.
in the original matrix, the roles of these matrices are reversed.- siteNames: list
- A list of site names. If left blank, site names are taken as the index of the pandas.DataFrame or the row index from the numpy.ndarray.
- spNames: list
- A list of species names. If left blank, species names are taken as the column names of the pandas.DataFrame or the column index from the numpy.ndarray.
- scaling: [1 | 2]
Which type of scaling to use when calculating site and species scores. 1 produces a site biplot, 2 produces a species biplot. In biplots, only the first two axes are shown. The plots are constructed as follows:
Four matrices are constructed. Outer species (column) locations on CA axes
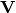 are given by the species (column) weights multiplied by the species (column) eigenvalues:
are given by the species (column) weights multiplied by the species (column) eigenvalues: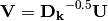
where
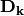 is a diagonal matrix of species (column) weights w_k. Likewise, outer site (row) locations are given by:
is a diagonal matrix of species (column) weights w_k. Likewise, outer site (row) locations are given by: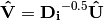
Inner site locations
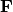 are given as:
are given as:
Inner species locations are given as:
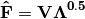
Scaling 1 Biplot: Scaling 1 shows the relationships among sites within the centroids of the species. This plot is useful for examining relationships among sites and how sites are composed of species. In this, the first two columns of inner site locations
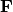 are plotted against the first two columns of the outer species locations
are plotted against the first two columns of the outer species locations 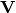 . NOTE: If
. NOTE: If 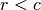 in the original matrix, this will be
in the original matrix, this will be 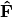 and
and 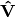 .
.Scaling 2 Biplot: Scaling 2 shows the relationships among species within the centroids of the sites. This plot is useful for examining relationships among species and how species are distributed among sites. In this, the first two columns of inner species locations
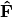 are plotted against the first two columns of the outer site locations
are plotted against the first two columns of the outer site locations 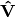 . NOTE: If
. NOTE: If 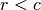 in the original matrix, this will be
in the original matrix, this will be 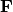 and
and 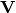 .
.
Attributes
-
w_col¶ Column weights in the proportion matrix. Normally species weights unless
 , in which case they are site weights.
, in which case they are site weights.
-
w_row¶ Row weights in the proportion matrix. Normally site weights unless
 , in which case they are species weights.
, in which case they are species weights.
-
U¶ Column (species) eigenvectors (see above note on transposition).
-
Uhat¶ Row (site) eigenvectors (see above note on transposition).
-
cumDesc_Sp¶ pandas.DataFrame of the cumulative contribution of each eigenvector to each species. Matrix
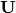 is scaled by eigenvalues
is scaled by eigenvalues 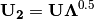 . Then, the cumulative sum of each column is divided by the column total for every row. If
. Then, the cumulative sum of each column is divided by the column total for every row. If 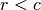 in the original data, then this operation is performed on
in the original data, then this operation is performed on 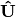 automatically.
automatically.
-
cumDesc_Site¶ The same for cumDesc_Sp, but for each site. Normally calculated for
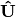 unless
unless 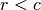 , then calculated on
, then calculated on 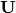 .
.
-
siteScores¶ Site scores along each CA axis. All considerations for matrix transposition and scaling have been taken into account.
-
spScores¶ Species scores along each CA axis. All considerations for matrix transposition and scaling have been taken into account.
Methods
-
classmethod
summary()¶ Returns a pandas.DataFrame of summary information for each correspondence axis, including SD’s (square-root of each eigenvalue), proportion of inertia explained, and cumulative inertia explained.
-
classmethod
biplot(coords=False, type=1, xax=1, yax=2, showSp=True, showSite=True, spCol='r', siteCol='k', spSize=12, siteSize=12, xlim=None, ylim=None)¶ Produces a biplot of the given CA axes.
- xax: integer
- Specifies CA axis to plot on the x-axis.
- yax: integer
- Specifies CA axis to plot on the y-axis.
- showSp: [True | False]
- Whether or not to show species in the plot.
- showSite: [True | False]
- Whether or not to show sites in the plot.
- spCol: string
- Color of species text.
- siteCol: string
- Color of site text.
- spSize: integer
- Size of species text.
- siteSize: integer
- Size of site text.
- xlim: list
- A list of x-axis limits to override default.
- ylim: list
- A list of y-axis limits to override default.
Examples
In Legendre and Legendre (2012), there is an example of three species varying among three lakes. Write in that data:
import ecopy as ep import numpy as np import pandas as pd Lakes = np.array([[10, 10, 20], [10, 15, 10], [15, 5, 5]]) Lakes = pd.DataFrame(Lakes, index = ['L1', 'L2', 'L3']) Lakes.columns = ['Sp1', 'Sp2', 'Sp3']
Next, run the CA:
lakes_CA = ep.ca(Lakes)
Check the variance explained by each CA axis (there will only be two):
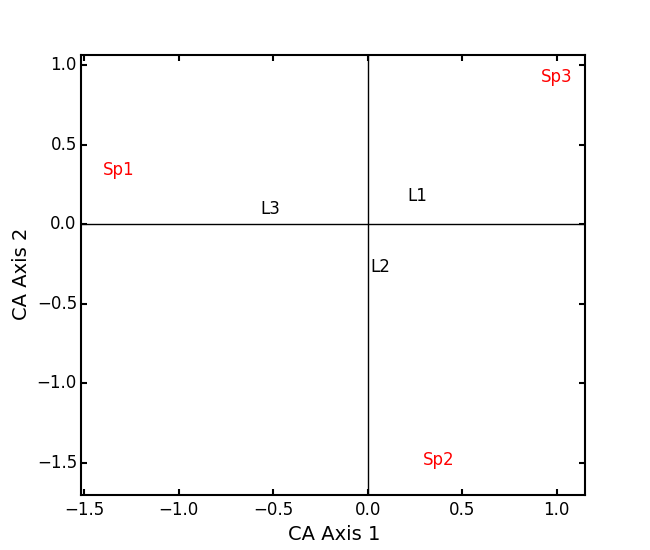
CA_summary = lakes_CA.summary() print(CA_summary) CA Axis 1 CA Axis 2 Std. Dev 0.310053 0.202341 Prop. 0.701318 0.298682 Cum. Prop. 0.701318 1.000000
Next, see how well the two axes explained variance in species and sites:
print(lakes_CA.cumDesc_Sp) CA Axis 1 CA Axis 2 Sp1 0.971877 1 Sp2 0.129043 1 Sp3 0.732340 1 print(lakes_CA.cumDesc_site) CA Axis 1 CA Axis 2 L1 0.684705 1 L2 0.059355 1 L3 0.967209 1
Make a Type 1 biplot to look at the relationship among sites:
lakes_CA.biplot()
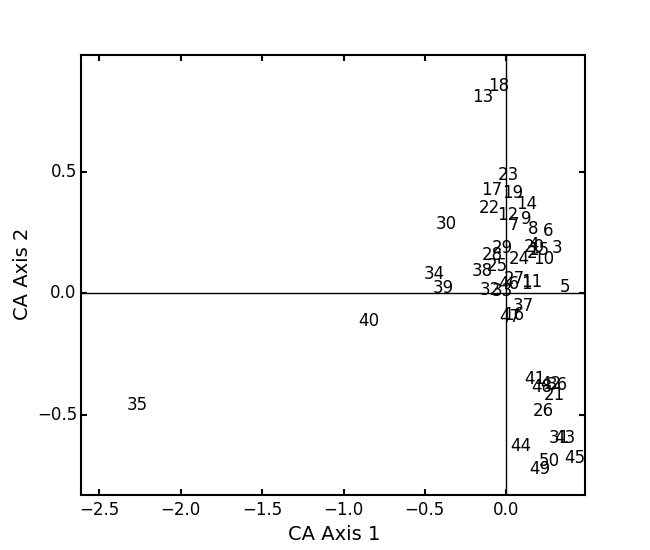
In a bigger example, run CA on the BCI dataset. NOTE: This is an example where
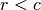 :
:BCI = ep.load_data('BCI') bci_ca = ep.ca(BCI) bci_ca.biplot(showSp=False)
-
class
pcoa(x, correction=None, siteNames=None)¶ Takes a square-symmetric distance matrix with no negative values as input. NOTE: This will not work with missing observations. Returns an object of class
pcoa.Parameters
- x: a numpy.ndarray or pandas.DataFrame
A square, symmetric distance matrix with no negative values and no missing observations. Diagonal entries should be 0.
For PCoA, distance matrix
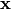 is first corrected to a new matrix
is first corrected to a new matrix 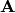 , where
, where 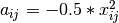 . Elements of the new matrix
. Elements of the new matrix 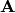 are centered by row and column means using the equation
are centered by row and column means using the equation 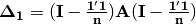 . PCoA is eigenanalysis of
. PCoA is eigenanalysis of 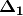 . Eigenvectors
. Eigenvectors 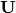 are scaled by the square root of each eigenvalue
are scaled by the square root of each eigenvalue 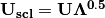 where
where 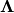 is a diagonal matrix of the eigenvalues.
is a diagonal matrix of the eigenvalues.- correction: [None | 1 | 2]
Which correction should be applied for negative eigenvalues. Accepts either ‘1’ or ‘2’ (must be a string). By default, no correction is applied.
Correction 1: Computes PCoA as described above. Adds the absolute value of the largest negative eigenvalue to the square original distance matrix (while keeping diagonals as 0) and then re-runs PCoA from the beginning.
Correction 2: Constructs a special matrix
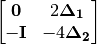
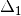 is the centered, corrected distance matrix as described above and
is the centered, corrected distance matrix as described above and 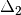 is a centered matrix (uncorrected) of
is a centered matrix (uncorrected) of 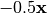 . The largest, positive eigenvalue of this matrix is then added the original distances and PCoA run from the beginning.
. The largest, positive eigenvalue of this matrix is then added the original distances and PCoA run from the beginning.- siteNames: list
- A list of site names. If not passed, inherits from the DataFrame index or assigns integer values.
Attributes
-
evals¶ Eigenvalues of each principle coordinate axis.
-
U¶ Eignevectors describing each axis. These have already been scaled.
-
correction¶ The correction factor applied to correct for negative eignvalues.
Methods
-
classmethod
summary()¶ Returns a pandas.DataFrame summarizing the variance explained by each principle coordinate axis.
-
classmethod
biplot(coords=False, xax=1, yax=2, descriptors=None, descripNames=None, spCol='r', siteCol='k', spSize=12, siteSize=12)¶ Produces a biplot of the given PCoA axes.
- coords: [True | False]
- If True, returns a dictionary of the plotted axes, where ‘Objects’ gives the coordinates of objects and ‘Descriptors’ gives the coordinates of the descriptors, if any.
- xax: integer
- Specifies PCoA axis to plot on the x-axis.
- yax: integer
- Specifies PCoA axis to plot on the y-axis.
- descriptors: numpy.ndarray or pandas.DataFrame
An n x m matrix of descriptors to plot on the biplot. These can be the original descriptors used to calculate distances among objects or an entirely new set. Descriptors must be quantitative. It will work for binary descriptors, but may be meaningless.
Given a new matrix
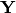 of descriptors, the matrix is standardized by columns to produce a new matrix
of descriptors, the matrix is standardized by columns to produce a new matrix 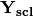 . The given principle coordinate axes denoted by xax and yax are placed into an n x 2 matrix
. The given principle coordinate axes denoted by xax and yax are placed into an n x 2 matrix 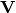 , which is also standardized by column. The covariance between the new descriptors and principle coordinates is given by
, which is also standardized by column. The covariance between the new descriptors and principle coordinates is given by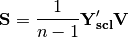
The covariance
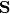 is then scaled by the eigenvalues corresponding to the given eigenvectors:
is then scaled by the eigenvalues corresponding to the given eigenvectors: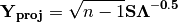
Matrix
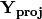 contains the coordinates of each descriptor and is what is returned as ‘Descriptors’ if coords=True.
contains the coordinates of each descriptor and is what is returned as ‘Descriptors’ if coords=True.- descripNames: list
- A list containing the names of each descriptor. If None, inherits from the column names of the pandas.DataFrame or assigned integer values.
- spCol: string
- Color of species text.
- siteCol: string
- Color of site text.
- spSize: integer
- Size of species text.
- siteSize: integer
- Size of site text.
-
classmethod
shepard(xax=1, yax=2)¶ Plots a Shepard diagram of Euclidean distances among objects in reduced space vs. original distance calculations. xax and yax as above.
Examples
Run PCoA on the ‘BCI’ data:
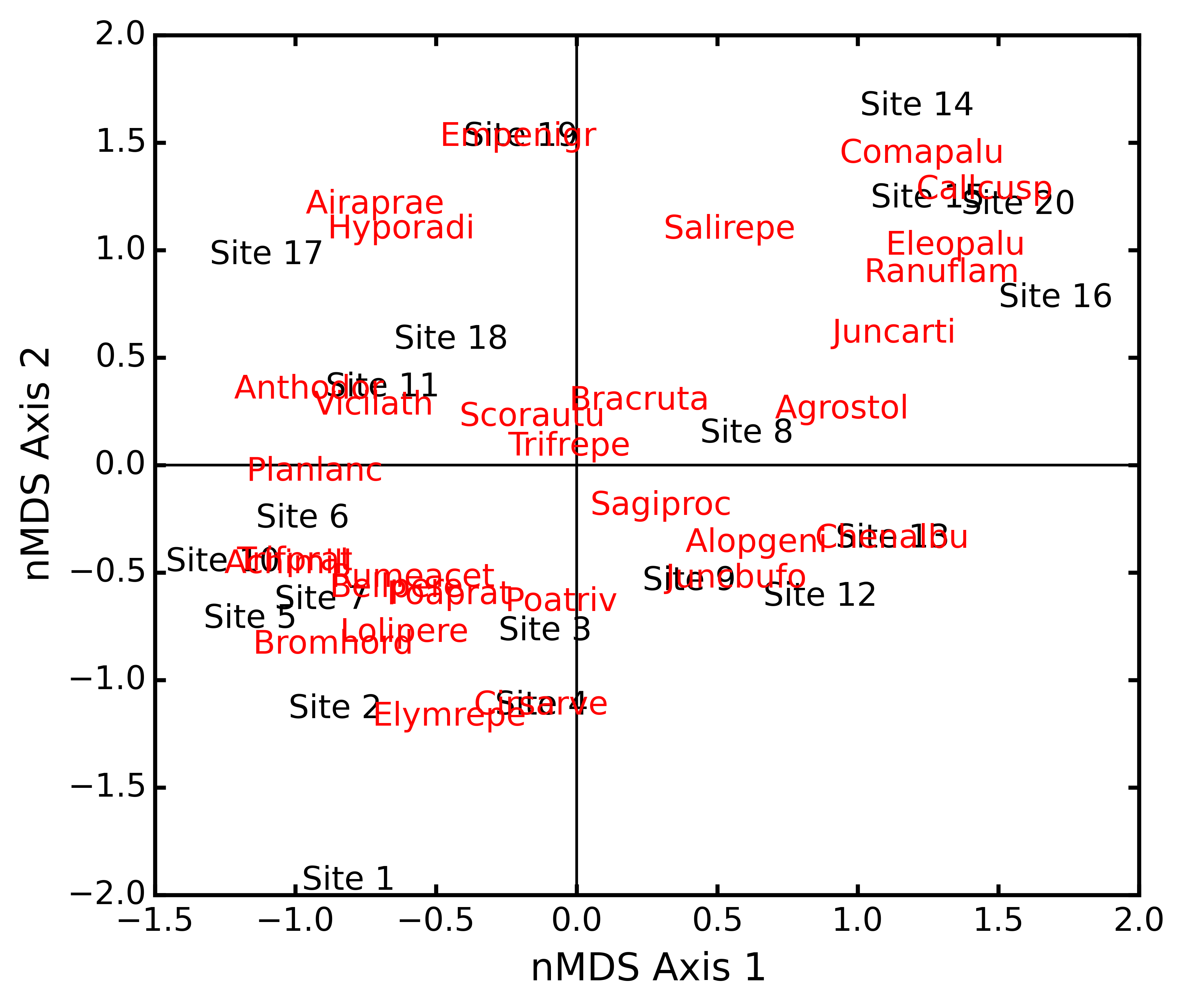
import ecopy as ep BCI = ep.load_data('BCI') brayD = ep.distance(BCI, method='bray', transform='sqrt') pc1 = ep.pcoa(brayD) print(pc1.summary()[['PCoA Axis 1', 'PCoA Axis 2']]) PCoA Axis 1 PCoA Axis 2 Std. Dev 1.094943 0.962549 Prop. 0.107487 0.083065 Cum. Prop. 0.107487 0.190552 pc1.biplot()
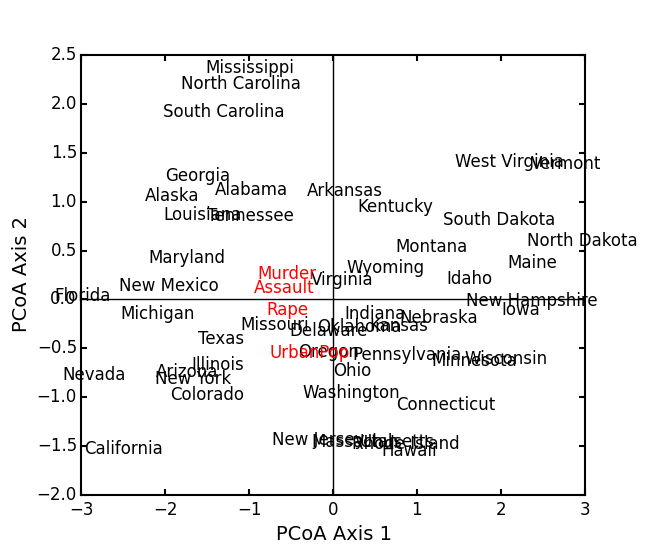
Attempting to show species on the above biplot results in a messy graph. To better illustrate its use, run PCoA on the USArrests data:
USA = ep.load_data('USArrests') USA.set_index('State', inplace=True) # standardize columns first USA = USA.apply(lambda x: (x - x.mean())/x.std(), axis=0) eucD = ep.distance(USA, 'euclidean') pc2 = ep.pcoa(eucD, siteNames=USA.index.values) pc2.biplot(descriptors=USA)
-
class
MDS(distmat, siteNames=None, naxes=2, transform='monotone', ntry=20, tolerance=1E-4, maxiter=3000, init=None)¶ Takes a square-symmetric distance matrix with no negative values as input. After finding the solution that provide the lowest stress, ecopy.MDS scales the fitted distances to have a maximum equal to the maximum observed distance. Afterwards, it uses PCA to rotate the object (site) scores so that variance is maximized along the x-axis. Returns an object of class
MDS.Parameters
- distmat: np.ndarray or pandas.DataFrame
- A square-symmetric distance matrix.
- siteNames: list
- A list of names for each object. If none, takes on integer values or the index of the pandas.DataFrame.
- naxes: integer
- Number of ordination axes.
- transform: [‘absolute’ | ‘ratio’ | ‘linear’ | ‘monotone’]
Which transformation should be used during scaling.
absolute: Conducts absolute MDS. Distances between points in ordination space should be as close as possible to observed distances.
ratio: Ordination distances are proportional to observed distances.
linear: Ordination distances are a linear function of observed distances. Uses the technique of Heiser (1991) to avoid negative ordination distances.
monotone: Constrains ordination distances simply to be ranked the same as observed distance. Typically referred to as non-metric multidimensional scaling. Uses isotonic regression developed by Nelle Varoquaux and Andrew Tulloch from scikit-learn.
- ntry: integer
- Number of random starts used to avoid local minima. The returned solution is the one with the lowest final stress.
- tolerance: float
- Minimum step size causing a break in the minimization of stress. Default = 1E-4.
- maxiter: integer
- Maximum number of iterations to attempt before breaking if no solution is found.
- init: numpy.ndarray
- Initial positions for the first random start. If none, the initial position of the first try is taken as the site locations from classical scaling, Principle Coordinates Analysis.
Attributes
-
scores¶ Final scores for each object along the ordination axes.
-
stress¶ Final stress.
-
obs¶ The observed distance matrix.
-
transform¶ Which transformation was used.
Methods
-
classmethod
biplot(coords=False, xax=1, yax=2, siteNames=True, descriptors=None, descripNames=None, spCol='r', siteCol='k', spSize=12, siteSize=12)¶ Produces a biplot of the given MDS axes.
- coords: [True | False]
- If True, returns a dictionary of the plotted axes, where ‘Objects’ gives the coordinates of objects and ‘Descriptors’ gives the coordinates of the descriptors, if any.
- xax: integer
- Specifies MDS axis to plot on the x-axis.
- yax: integer
- Specifies MDS axis to plot on the y-axis.
- descriptors: numpy.ndarray or pandas.DataFrame
- A matrix of the original descriptors used to create the distance matrix. Descriptors (i.e. species) scores are calculated as the weighted average of site scores.
- descripNames: list
- A list containing the names of each descriptor. If None, inherits from the column names of the pandas.DataFrame or assigned integer values.
- spCol: string
- Color of species text.
- siteCol: string
- Color of site text.
- spSize: integer
- Size of species text.
- siteSize: integer
- Size of site text.
-
classmethod
shepard(xax=1, yax=2)¶ Plots a Shepard diagram of Euclidean distances among objects in reduced space vs. original distance calculations. xax and yax as above.
-
classmethod
correlations()¶ Returns a pandas.Series of correlations between observed and fitted distances for each site.
-
classmethod
correlationPlots(site=None)¶ Produces a plot of observed vs. fitted distances for a given site. If site=None, then all sites are plotted on a single graph.
Examples
Conduct nMDS on the ‘dune’ data:
import ecopy as ep dunes = ep.load_data('dune') dunes_T = ep.transform(dunes, 'wisconsin') dunes_D = ep.distance(dunes_T, 'bray') dunesMDS = ep.MDS(dunes_D, transform='monotone')
Plot the Shepard diagram:
dunesMDS.shepard()
Check the correlations for observed vs. fitted distances:
dunesMDS.correlationPlots()
Make a biplot, showing species locations:
dunesMDS.biplot(descriptors=dunes_T)
-
class
hillsmith(mat, wt_r=None, ndim=2)¶ Takes an input matrix and performs ordination described by Hill and Smith (1976). Returns an object of class
hillsmith, with several methods and attributes. NOTE: This will NOT work when rows < columns or with missing values.Parameters
- mat: pandas.DataFrame
- A matrix for ordination, where objects are rows and descriptors/variables as columns. Can have mixed data types (both quantitative and qualitative). If all columns are quantitative, this method is equivalent to PCA. If all columns are qualitative, this method is equivalent to MCA. Should not be used with ordered factors. In order to account for factors, this method creates dummy variables for each factor and then assigns weights to each dummy column based on the number of observations in each column.
- wt_r: list or numpy.ndarray
- Optional vector of row weights.
- ndim: int
- Number of axes and components to save.
Attributes
-
evals¶ Eigenvalues in order of largest to smallest.
-
pr_axes¶ The principle axes of each column.
-
row_coords¶ Row coordinates along each principle axis.
-
pr_components¶ The principle components of each row.
-
column_coords¶ Column coordinates along each principle component.
Methods
-
classmethod
summary()¶ Returns a data frame containing information about the principle axes.
-
classmethod
biplot(invert=False, xax=1, yax=2, obsNames=True)¶ Create a biplot using a specified transformation.
- invert: [True|Fasle]
- If False (default), plots the row coordinates as points and the principle axes of each column as arrows. If True, plots the column coordinates as points and the principle components of each row as arrows.
- xax: integer
- Specifies which PC axis to plot on the x-axis.
- yax: integer
- Specifies which PC axis to plot on the y-axis.
- obsNames: [True | False]
- Denotes whether to plot a scatterplot of points (False) or to actually show the names of the observations, as taken from the DataFrame index (True).
Examples
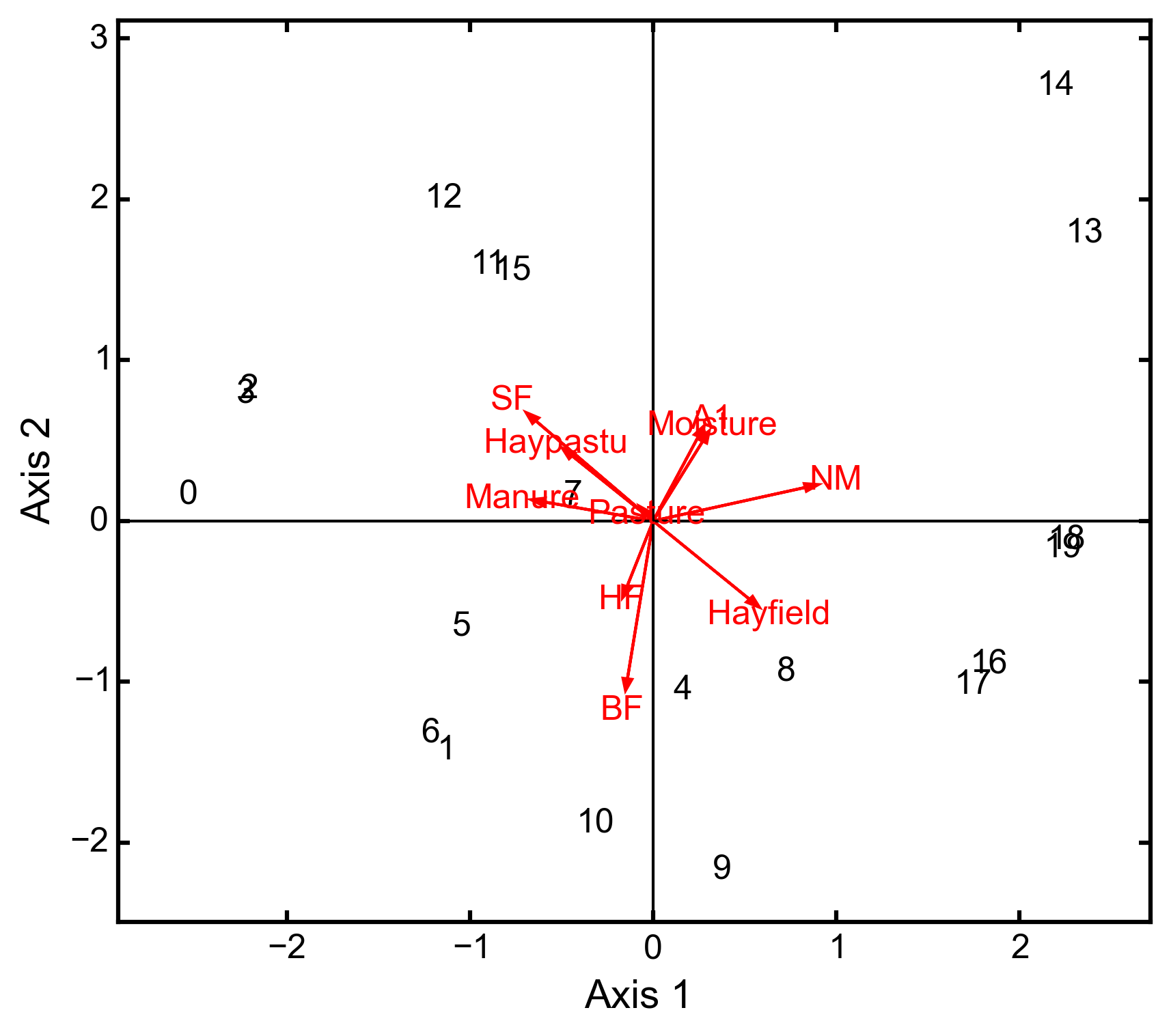
Hill and Smith analysis of the dune_env data:
import ecopy as ep dune_env = ep.load_data('dune_env') dune_env = dune_env[['A1', 'Moisture', 'Manure', 'Use', 'Management']] print(ep.hillsmith(dune_env).summary().iloc[:,:2]) Axis 1 Axis 2 Std. Dev 1.594392 1.363009 Prop Var 0.317761 0.232224 Cum Var 0.317761 0.549985 ep.hillsmith(dune_env).biplot(obsNames=False, invert=False)
-
ord_plot(x, groups, y=None, colors=None, type='Hull', label=True, showPoints=True, xlab='Axis 1', ylab='Axis 2')¶ Delineates different groups in ordination (or regular) space.
Parameters
- x: numpy.ndarray, pandas.DataFrame, pandas.Series (required)
- Coordinates to be plotted. Can be either a one or two column matrix. If only one column, then y must be specified.
- groups: list, pandas.DataFrame, pandas.Series (required)
- Factor denoting group identification
- y: numpy.ndarray, pandas.DataFrame, pandas.Series
- y coordinates to be plotted. Can only have one column, and must be specified is x is only one column.
- colors: string, list, pandas.Series, pandas.DataFrame
- Gives custom colors for each group. Otherwise default colors are used.
- type: [‘Hull’ | ‘Line’]
- ‘Hull’ produces a convex hull, whereas ‘Line’ produces lines connected to the centroid for each point.
- label: [True | False]
- Whether or not a label should be shown at the center of each group.
- showPoints: [True | False]
- Whether or not the points should be shown.
- xlab: string
- Label for the x-axis.
- ylab: string
- Label for the y-axis.
Example
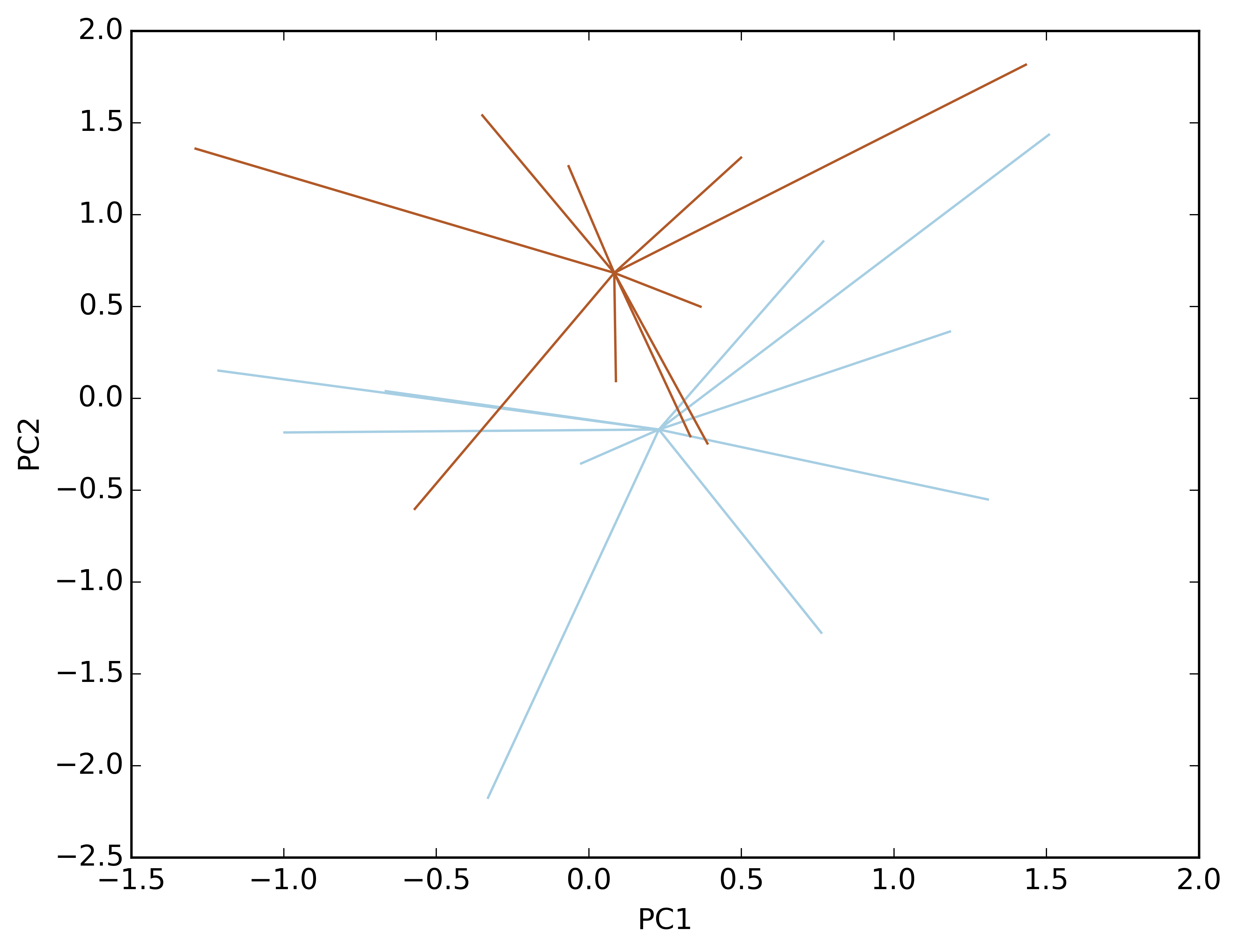
Generate fake data simulating ordination results:
import numpy as np import ecopy as ep import matplotlib.pyplot as plt nObs = 10 X = np.random.normal(0, 1, 10*2) Y = np.random.normal(0, 1, 10*2) GroupID = ['A']*nObs + ['B']*nObs Z = np.vstack((X, Y)).T
Make a convex hull plot where groups are red and blue:
ep.ord_plot(x=Z, groups=GroupID, colors=['r', 'b'])
Make a line plot with coordinates in different matrices. Remove the points and the labels:
ep.ord_plot(x=X, y=Y, groups=GroupID, type='Line', xlab='PC1', ylab='PC2', showPoints=False, label=False)